home || posta || verifiche on line || foglio elettronico || ricerca || calendario
	Misura dell'area dell'ellisse

13 Febbraio 2002

Approssimazione dell'area dell'ellisse con metodo stocastico

Data l'equazione dell'ellisse in forma canonica

x^2/a^2+y^2/b^2=1

vogliamo approssimarne l'area "bombardando" con una pioggia casuale di punti il rettangolo che contiene la curva nel primo quadrante. Tale rettangolo è di dimensioni a e b e perciò la misura dell'area sarà ab.

Il rapporto fra il numero di punti che cadranno all'interno sul totale dei punti generati è lo stesso del rapporto delle misure delle aree del quarto di ellisse con quello del rettangolo. Posto n il numero di punti interni alla conica e N il numero totale di punti si ha la proporzione 

n : N = Area quarto di ellisse : Area rettangolo

dalla quale si ricava

Area ellisse = 4 n/N a b

Il calcolo di n in funzione di N lo si può implementare in modo efficiente con il foglio elettronico di cui riporto le formule:

Si potrà verificare che il rapporto nella cella E7 non dipende dai valori di a e b (pertanto la misura dell'area dipenderà esclusivamente da a e b oltre che dal rapporto in questione). 

Qualche esempio:

Esempio 1
Esempio 2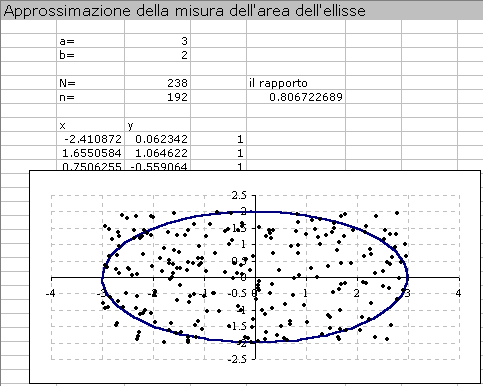

Premendo F9 possiamo generare nuove "piogge" e verificare che il rapporto oscilla attorno al valore di 0.75 circa.

Vogliamo ora implementare un numero significativo di casi: in ambiente VBA digitiamo la funzione:

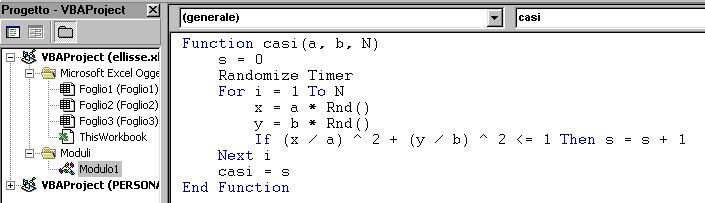
e generiamo su un secondo foglio la seguente tabella:

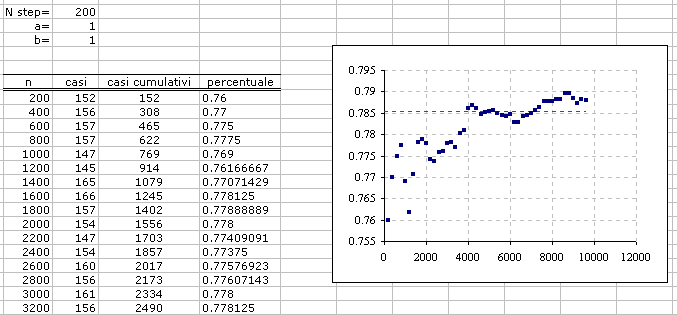
continua...

dove Nstep rappresenta il valore di N da passare alla funzione "casi". Si verifica ancora che il "limite" della successione delle percentuali non dipende dai valori a e b della conica e si stabilizza sul valore della linea rossa tratteggiata. Ecco una seconda simulazione

Ti interessa il file? SCARICALO e fanne buon uso!

home || posta || verifiche on line || foglio elettronico || ricerca