home || posta || verifiche on line || foglio elettronico || ricerca || calendario
	Spettro di un segnale periodico

Il foglio elettronico che ho realizzato si propone di approssimare i coefficienti di una serie di Fourier attraverso l'integrazione definita e approssimata con il metodo dei rettangoli dei coefficienti: tale metodo, pur non essendo il più efficiente, è comunque il più significativo dal punto di vista didattico. Nulla vieta che i ragazzi possano in un secondo momento implementare lo stesso foglio con metodi di ordine superiore.

In tal senso ho utilizzato il foglio elettronico Excel (c) con le relative macro in Visual Basic. Innanzitutto serve un "interprete" per l'espressione del segnale che verrà digitato sulla cella del foglio: in un modulo del VB (che si apre con ALT+F11) si digita

In seguito ho implementato le funzioni per il calcolo dei coefficienti a_n e b_n della serie, per la cui definizione rimando a un qualunque libro di testo sull'argomento

NOTA: come si può estrapolare dal codice, il semiperiodo T viene considerato pi greco quando è omesso.

Partendo ora dai coefficienti dello spettro è possibile ricostruire il segnale con la funzione

Ora vediamo il foglio elettronico: per i dati di ingresso, evidenziati con lo sfondo grigio sono necessari:

• una cella per la scrittura del segnale periodico in funzione di t (e non di x o altro)

• il semiperiodo T (se omesso viene considerato pi greco)

• il numero di suddivisioni "N rett" per il calcolo dell'integrale definito con il metodo dei rettangoli (100 è mediamente sufficiente)

• il numero delle armoniche "Nmax" che si vogliono approssimare

Ecco come si presenta:

La struttura per la costruzione della tabella dello spettro è la seguente:

Si noti che variando una delle celle "in grigio" il foglio si aggiorna (non molto velocemente, peraltro) e sul grafico vengono mostrate le curve del segnale e la ricostruzione in base allo spettro di Fourier.

Qualche esempio:

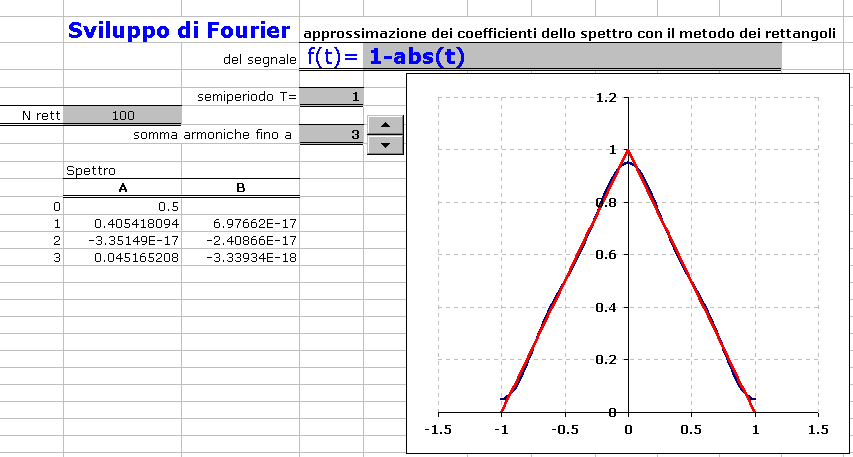
Se sei interessato per fini didattici o di studio al file di Excel completo, clicca qui.

home || posta || verifiche on line || foglio elettronico || ricerca