![]()
Su una mappa di pirati (o corsari) sta scritto: (tra [ ] le mie traduzioni)
"Lancia una foglia leggera al vento e lassa che si posi sul prato
[...dell'isola del tesoro].
Ove ella si poserÓ posiziona te istesso e da lý volgiti e conta i passi in
direzione della betulla. Svolta a destra di un angolo orto [retto] e percorri in
tale direzzione lo istesso numero di passi. In dove arriverai pianta un bastone.
Returna alla folia caduta e fai l'istessa cosa verso la quercia, dove girerai
per la mancina parte [... sinistra ...] e inficcherai nella terra un altro
bastone. Ebbene: lo tesoro si trova nel punto mediano fra i due bastoni"
Ma questo (benedetto) tesoro Ŕ sempre nello "istesso" punto
o cambia dal punto in cui cade la foglia?
In altre parole: le indicazioni della mappa sono SUFFICIENTI a determinare in
maniera univoca il tesoro o no?
![]()
Ecco finalmente la soluzione del quesito del tesoro dei pirati:
Ponendo la betulla nella posizione (0,0) la quercia nella posizione (L,0), dove L rappresenta la distanza fissa tra i due alberi, chiamiamo con (x,y) il punto dove cade la foglia. Ebbene: per determinare la posizione dei due paletti possiamo utilizzare i triangoli rettangoli colorati ruotandoli e traslandoli come in figura
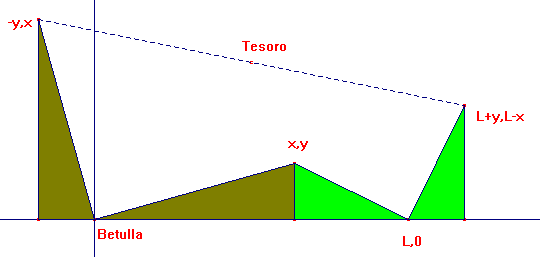
Il punto medio fra (-y,x) e (L+y,L-x) Ŕ sempre il punto (L/2, L/2) indipendentemente dal punto (x,y) in cui cade la foglia.
Bello, no?
![]()