Legge del raffreddamento di Newton
Chiamata con y(t) la funzione che esprime la temperatura di
un corpo all’istante t, in un sistema isolato a temperatura esterna costante 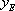 in base alla legge del raffreddamento di Newton si ha il sistema differenziale
in base alla legge del raffreddamento di Newton si ha il sistema differenziale
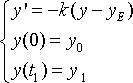
La risoluzione analitica del problema di Cauchy si basa sul fatto che l’equazione differenziale è a variabili separabili e pertanto

Se 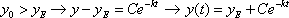
Imponendo che all’istante iniziale la temperatura sia  si ottiene che
si ottiene che
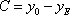 Per determinare il valore del parametro k si utilizza la terza condizione del
sistema
Per determinare il valore del parametro k si utilizza la terza condizione del
sistema 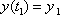 e risolvendo rispetto al parametro stesso si
ottiene
e risolvendo rispetto al parametro stesso si
ottiene

Pertanto l’equazione della legge della temperatura diventa
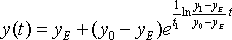
Nella animazione sottostante è possibile spostare con il mouse i punti azzurri e verificare l’andamento della soluzione.
Buona interazione!
5 agosto 2008, creato con il mitico GeoGebra